Kinetics of the release of silicon and aluminium from aluminosilicates into aqueous mildly acid solutions

Jiří Faimon

Department of Mineralogy, Petrography and Geochemistry, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic

předloženo 16.května 1997; k tisku doporučil Tomáš Lánczos

Keywords: aluminosilicates, Al and Si fluxes, kinetics, modeling

Abstract

The release of Si and Al from feldspar, granodiorite and amphibolite into mildly acid solutions was investigated during long-term laboratory batch experiments. A simple kinetic model, including dissolution of surface defects and precipitation of secondary solids, was proposed. The rate constants for fluxes of Si and Al in and out from solution were estimated on the basis of the model. They are summarized as follow:

The fluxes of silicon from the aluminosilicates increase in the sequence feldspar - granodiorite - amphibolite. The fluxes of aluminium seem to follow the opposite trend. The release of Si and Al from feldspar is non-stechiometric. The fluxes of Al from solution into secondary solids greatly exceed the fluxes of Si.

Introduction

The release of elements into aqueous environment during weathering of aluminosilicate rocks is an important geochemical phenomenon. It controls composition of natural waters and participates in the formation of secondary solids and, eventually, in redistribution of elements in the earth crust. Many authors have studied experimentally the weathering of aluminosilicates (see, e.g. Aagaard and Helgeson 1982, Helgeson et al. 1984, and references mentioned therein). They interpreted their data at first phenomenologically by use of parabolic kinetics (e.g. Busenberg and Clemency 1976, Grandstaff 1977). Later, considering that the weathering was controlled by surface reaction, they modeled the results on the basis of the transition state theory (Lasaga 1981a, Aagaard and Helgeson 1982). In the presented work, in contrast, there is applied the model of mass reservoirs and fluxes among them (see Lasaga 1981b).

Experimental

Samples

The studied samples of granodiorite, amphibolite and feldspar come from Brno-Řečkovice, Želešice and Věžná (Moravia, Czech Republic), respectively. The samples were crushed, ground, wet sieved, and, finally, washed three times with distilled water. The resultant grains, about 100 m m in sizes, were used for dissolution experiments. The purity of the samples and the grain size were checked by scanning electron microscope (CamScan4-DV) coupled with energy dispersive X-ray spectrometer (LINK AN 10000).

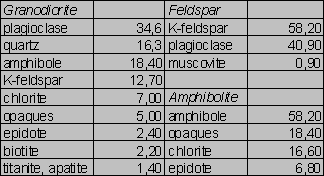
Tab.1. Modal analyses of the samples (vol. %)

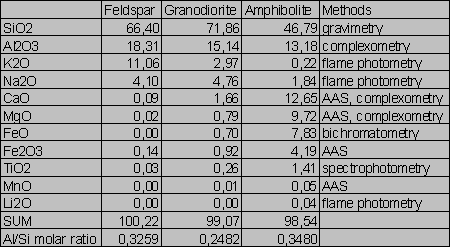
Tab.2. Wet analyses of the samples (wt %)

Compositions of the samples are given in Tabs.1-2. The Si/Al molar ratios are presented in Tab.2. Average densities and surface areas of the samples are reported in Tab.3. The specific densities were measured by means of a pycnometer. The areas were computed on the basis of geometrical considerations (Parks 1990).

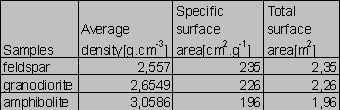
Tab.3. Densities and surface areas of the samples

Weathering

Two parallel runs of experiments were conducted for each sample: 100g of granodiorite, feldspar, and amphibolite were placed into plastic bottles that were filled with 1500 ml solution of initial pH ~ 3 (H₂SO₄). The weathering was proceeding in open system at ambient conditions. The mixtures were agitated by hand once a day. The pH, after initial increase, was maintained within a close range of values due to buffering of the solutions by the air CO₂.

Analyses of solutions

pH of the solutions was measured by a glass electrode SEO 212 (Sultech) combined with the pH-meter OP 2 (Radelkis Budapest). The 10 ml aliquots were pipeted from the solutions and filtered through a membrane filters (ME 28/41ST - 1.2 m m nominal pore size) to remove particles (disintegrated primary grains, secondary solids). The filtrates were analyzed for Al and Si concentrations using ICP-ES (UNICAM PU 7000).

Results

Experimental kinetics of the release of Si and Al at the given ranges of pH is plotted in Figs.1-3. Provided that the weathering of aluminosilicates is controlled by a surface irreversible reaction, the rate of dissolution should be constant and independent on the solution composition. Thus, the kinetics should result in a linear plot of the concentration vs. time. The conspicuous curvature of the plots (Fig.1-3) can be explained (1) by decreasing dissolution rate during the experiment and/or (2) by fluxes of elements out away from the solutions.

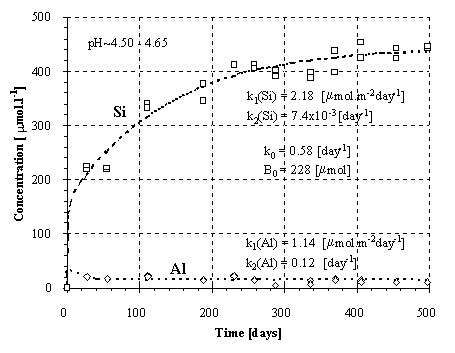
Fig.1.: Kinetics of the Si and Al release from the granodiorite.

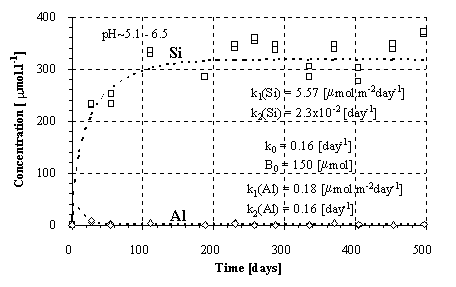
Fig.2.: Kinetics of the Si and Al release from the amphibolite.

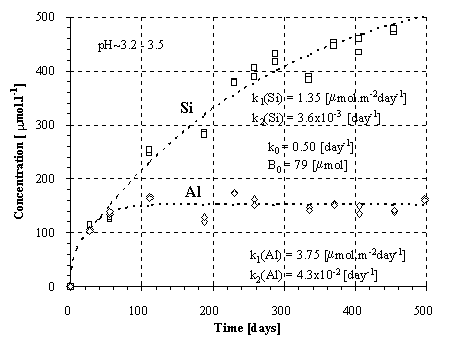
Fig.3.: Kinetics of the Si and Al release from the feldspar.

(1) Dissolution rates found experimentally in laboratory often seem to be unrealistically high (Velbel 1985, 1993). There is a hypothesis (e.g. Eggleston et al. 1989) suggesting that the rates are affected by dissolution of surface defects with high reactivity. These defects probably arise during sample preparation, i.e. during crushing or grinding. The decreasing rate of dissolution can be result of gradual destruction of the defects. Some authors (Chou and Wollast 1984, Knaus and Wolery 1986, 1988) studied the weathering kinetics in flow-through reactors. They found that the rate of dissolution was decreasing during initial stages of the experiments and then was constant after approximately thirty days. Thus, it seems reasonable to presume that the dissolution of the defects affects the dissolution kinetics only within the first 30 days of the experiment.

(2) In the course of the experiments, the solutions can attain supersaturation with gibbsite and kaolinite (Faimon 1995). Consequently, Al and Si can ”flow out” from the solution forming these minerals or their amorphous equivalents. In fact, the precipitation of secondary solids was observed after 20th day of the experiment and, of course, it could modify the shape of the kinetic curve from this time.

On the basis of the former considerations, a simple kinetic model was proposed (Fig.4). It consists of three main reservoirs: primary rock, solution, and secondary solids. The rock reservoir consists of the rock with the ”old” surface (A) and the rock with the surface defects (B). Assuming that the system is far from the thermodynamic equilibrium, the fluxes among the reservoirs are expressed by one-way arrows. k₀, k₁, and k₂ are rate constants.

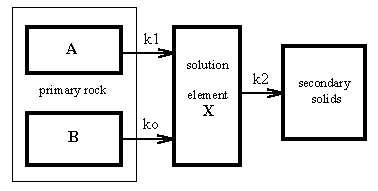
Fig.4.: A three-reservoir model of the release of an element X from rock. (A) and (B) are amounts of rock with the ”old” surface and with the surface defects, respectively. The fluxes of element X are expressed by the one-way arrows and quantified by the rate constants k₁, k₀, and k₂.

If the rate of flow of X from reservoir is directly proportional to the reservoir content, the model behavior can be described by the differential equations (1,2)

, (1)

, (2)

where X is the amount of the released element in the reservoir, B is amount of the rock with surface defects, and A is the total surface area of the primary rock. k₀, k₁, and k₂ are the rate constants quantified the fluxes of X from the surface defects, from the primary rock, and from the solution into secondary solids, respectively.

If A is constant and B₀ is the initial content of the rock reservoir B, then the solution of the equations (1,2) gives for X

. (3)

For concentration of a released element X, eqn. (3) yields

, (4)

where [X] is the concentration of the released element and V is the volume of the used solution.

Now, we can fit the experimental data by the function (4), using the method of last squares. The known parameters are: V ~ 1.5 liter; the total surface areas A of the granodiorite, amphibolite, and feldspar ~ 2.26, 1.96, and 2.35 m², respectively. We can find the parameters k₀, B₀, k₁ and k₂, solving the expression (5) for the {X_i,t_i} data set so that the sum of squares is minimum.

(5)

The solution was found numerically by Newton method, using the computer program MS Excel - Solver. The parameters k₀ and B₀ were found solely for the Si fluxes and then applied for the Al fluxes, because of the low Al concentrations and difficulties during modeling. For amphibolite, the method of last squares did not yield unambiguous results. This failure can be attributed to an effect of nonlinear phenomena on aqueous concentrations (Faimon 1996) and following scattering of the experimental points (see Fig.2). Therefore, only the constants k₀, k₁ and k₂ were found and B₀ was estimated from the shape of the curve. The resulting rate constants and B₀ are given in Tab.4. The constant k₁(Si) and k₁(Al) relate to the fluxes of Si and Al from the primary rock, respectively. The constants k₂(Si) and k₂(Al) relate to the fluxes of Si and Al into the secondary solids, respectively.

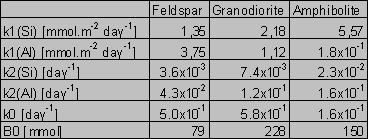
Tab.4. The found rate constants and B₀ (for details, see text)

It should be emphasized that the constants are pH-dependent and that they apply only for the given range of pH. The dependency (4) with the corresponding constant k₀, B₀, k₁ and k₂ fits the experimental points in Figs. 1-3.

We can verify the found values of the rate constants comparing our data for feldspar with the data given by other authors. If the total rate of the feldspar dissolution relates to 1/3 of the rate of the Si release, the resulting constant for the feldspar dissolution will be 0,45 mmol.m^-2 day^-1, i.e. 5.2x10^-16 mmol.cm^-2 s^-1. This is consistent with the commonly accepted value for feldspar dissolution (see the survey of Helgeson et al., 1984).

Discussion

The values of the rate constant k₁ for the Si release (Tab.4) increase in the sequence feldspar - granodiorite - amphibolite. The values of k₁ for the Al release follow the opposite trend. However, there is, especially for the amphibolite, high uncertainty in the values of k₁ due to the extremely low Al concentrations for modeling (see Fig.2).

Tab. 5. Ratios of rate constants

There are given ratios of the rate constants in Tab.5. Only the k₁(Al):k₁(Si) ratio for the granodiorite dissolution (0.51) approaches the granodiorite Al/Si molar ratio (0.25), compare with Tab.2. The k₁(Al):k₁(Si) for dissolution of the amphibolite and feldspar very differ from the Al/Si molar ratios of the samples. The k₁(Al):k₁(Si) for the amphibolite dissolution (3.23x10^-2) is one order of magnitude lower than the amphibolite Al/Si molar ratio (0.35). In contrast, the k₁(Al):k₁(Si) ratio for feldspar (2.78) is one order of magnitude higher than the stoichiometric one (0.33). This indicates a feldspar non-stoichiometric dissolution. In fact, the preferential release of Al from feldspar into acid solutions is consistent with the findings of many authors (Hellmann et al. 1990, Muir et al. 1989, 1990, Inskeep et al. 1991, Casey et al. 1989).

The high k₂(Al):k₂(Si) ratios suggest that the fluxes of Al out away from solutions widely exceed the Si fluxes. This is consistent with thermodynamic considerations that predict the predominating precipitation of Al-solids until the Si concentration of the gibbsite/kaolinite equilibrium is approached.

Conclusions

Kinetics of the release of silicon and aluminium from granodiorite, amphibolite, and feldspar into aqueous mildly acid solution was studied during long-term laboratory batch experiments. A new kinetic model was proposed. It includes as phenomena as the dissolution of surface defects and the formation of secondary solids. The theoretical dependencies derived from the model fit well the experimental data. As the found values of the rate constants show, the Si fluxes from aluminosilicates into solutions increase in the sequence feldspar - granodiorite - amphibolite. In contrast, the Al fluxes seem to follow an opposite trend. The flux of Al from amphibolite, compared with the Si flux, is lower than the amphibolite Al/Si molar ratio suggests. The flux of Al from feldspar, on the other hand, is extremely high and exceeds the Si flux, which indicates a feldspar non-stoichiometric dissolution. The fluxes of Al from solutions into secondary solids widely exceed the Si fluxes in all experiments.

Acknowledgements

I would like to thank Dr. Sulovský and Mgr. Vávra for performing SEM and EDXR analyses, Dr. Gregerová for modal analyses, Dr. Zeman for discussions and Dr. Němec for reading the manuscript.

References

Aagaard P., Helgeson H.C. (1982): Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. I. Theoretical considerations. - Amer. J. Sci., 282, 237-285.

Busenberg E., Clemency C.V. (1976): The dissolution kinetics of feldspars at 25^oC and 1 atm CO₂ partial pressure. - Geochim. Cosmochim. Acta, 40, 41-49.

Casey W.H., Westrich H.R., Massiv T., Banfield J.F., and Arnold G.V. (1989): The surface of labradorite feldspar after acid hydrolysis. Chem. Geol., 78, 205-218.

Chou L. and Wollast R. (1984): Study of the weathering of albite at room temperature and pressure with a fluidized bed reactor. Geochim. Cosmochim. Acta, 48, 2205-2217.

Eggleston C.M., Hochella Jr.M.F., and Parks G.A. (1989): Sample preparation and aging effect on the dissolution rate and surface composition of diopside. - Geochim. Cosmochim. Acta 53, 797-804.

Faimon J. (1995): Formation of colloids during silicate weathering. Ph.D. thesis, Masaryk Univ., Brno (in Czech).

Faimon J. (1996): Oscillatory silicon and aluminum aqueous concentrations during experimental aluminosilicate weathering. Geochim. Cosmochim. Acta, 60, 2901-2907.

Grandstaff D.E. (1977): Some kinetics of bronzite orthopyroxene dissolution. Geochim. Cosmochim. Acta, 41, 1097-1103.

Helgeson H.C., Murphy W.M., Aagaard P. (1984): Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions. II. Rate constants, effective surface area, and the hydrolysis of feldspar. - Geochim. Cosmochim. Acta, 48, 2405-2432.

Hellmann R., Eggleston C.M., Hochella Jr. M.F., and Crerar D.A. (1990): The formation of leached layers on albite surfaces during dissolution under hydrothermal conditions. Geochim. Cosmochim. Acta, 54, 1267-1281.

Inskeep W.P., Nater E.A., Bloom P.R., Van der Voort D.S., and Erich M.S. (1991): Characterization of laboratory weathered labradorite surfaces using X-ray photoelectron spectroscopy and transmission electron microscopy. Geochim. Cosmochim. Acta, 55, 787-800.

Knauss K.G. and Wolery T.J. (1986): Dependence of albite dissolution kinetics on pH and time at 25^oC and 70^oC. Geochim. Cosmochim. Acta, 50, 2481-2497.

Knauss K.G. and Wolery T.J. (1988): The dissolution kinetics of quartz as a function of pH and time at 70^oC. Geochim. Cosmochim. Acta, 52, 43-53.

Muir I.J., Bancroft G.M., and Nesbitt H.W. (1989): Characteristics of altered labradorite surfaces by SIMS and XPS. Geochim. Cosmochim. Acta, 53, 1235-1241.

Muir I.J., Bancroft G.M., Shotyk W., and Nesbit H.W. (1990): A SIMS and XPS study of dissolving plagioclase. Geochim. Cosmochim. Acta, 54, 2247-2256.

Lasaga A.C. (1981a): Transition state theory. In: Kinetics of geochemical processes. - Review in mineralogy, 8, 135-169. Eds.: A.C.Lasaga, R.J.Kirkpatrick.

Lasaga A.C. (1981b): Dynamic treatment of geochemical cycles: Global kinetics. In: Kinetics of geochemical processes. Review in mineralogy, 8, 69-110. Eds.: A.C.Lasaga, R.J.Kirkpatrick.

Parks G.A. (1990): Surface energy and adsorption at mineral-water interfaces: An introduction. In: Mineral-Water Interface Geochemistry (ed. M. F. Hochella Jr. and A.F. White). Rev. Mineral., 23, 133-175.

Velbel M.A. (1985): Geochemical mass balances and weathering rates in forested watersheds of the southern Blue Ridge. - Am. J. Sci., 285, 904-930.

Velbel M.A. (1993): Constancy of silicate-mineral weathering-rate ratios between natural and experimental weathering: implications for hydrologic control of differences in absolute rates. - Chem. Geol., 105, 89-99.