Transformační matice

Krystalografické transformace můžeme chápat jako změnu polohy bodu o souřadnicích x, y, z pomocí operace symetrie do nové polohy x´, y´, z´ v rámci jedné ortogonální souřadné soustavy, nebo jako transformaci souřadné soustavy os x, y, z na osy x´, y´, z´.

Z lineárních transformací se v krystalografii uplatňují pouze transformace izometrické, tj. takové, kde nedochází ke změně vzdálenosti mezi dvěma body před a po transformaci. Libovolnou izometrickou transformaci můžeme vyjádřit matematicky pomocí tzv. transformační matice. Pro takovou operaci je transformační matice vždy ortogonální.

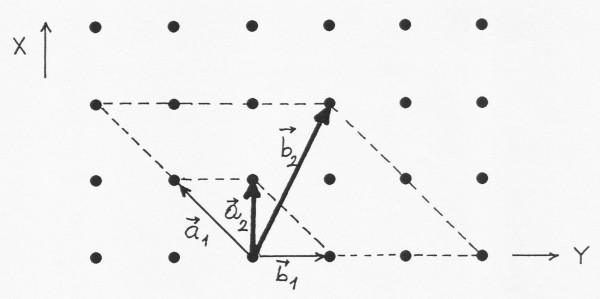
Sestavení transformační matice si můžeme demonstrovat na jednoduchém příkladu. Vyjádřeme „nové“ vektory přímé mřížky a₂ b₂ c₂ pomocí starých vektorů a₁ b₁ c₁. Z následujícího obrázku snadno odvodíme transformační rovnice, kdy vektor c₁ je kolmý na nákresnu (x, y) a je totožný s vektorem c₂.

a₂ = 1a₁ + 1b₁ + 0c₁

b₂ = 2a₁ + 3b₁ +0c₁

c₂ = 0a₁ + 0b₁ +1c₁

V maticovém vyjádření označíme námi vytvořenou matici jako transformační matici S.

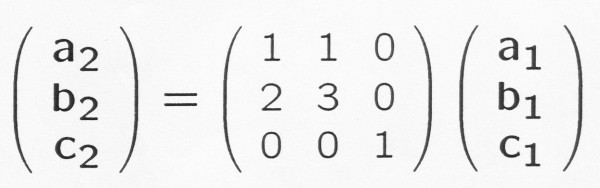
Známe-li transformační matici S, můžeme užitím inverzní matice S^-1 = T vyjádřit staré vektory a₁, b₁ a c₁ pomocí nových a₂, b₂ a c₂. K sestavení matice T je nutné stanovit potřebné doplňky S_ij a det S. Výsledná matice bude mít tvar:

                 3  -1   0
T = S-1 =  -2   1   0
                      0   0   1